Heap

Binary trees

Definition

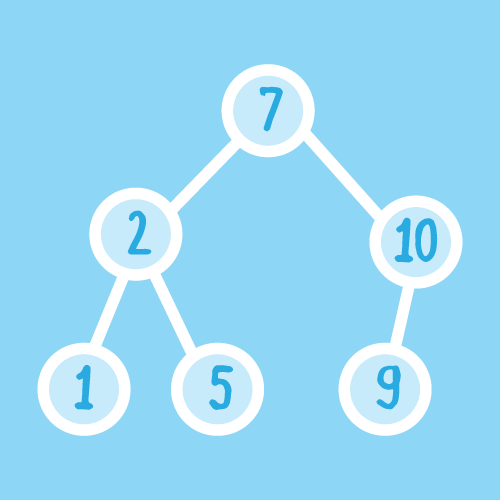 A binary tree is a tree that is either empty or consists of a root node and two disjoint binary trees called the left subtree and the right subtree, respectively.

Special classes:

 1) STRICT BINARY TREES are binary trees where every vertex has either 0 or 2 offspring.
2) FULL BINARY TREES are binary trees that have 2^k-1 vertices arranged on levels 0,1, ...,k-1, such that on each level i there are 2^i vertices.
3) COMPLETE BINARY TREES are binary trees obtained from a full binary tree by right-to-left elimination of nodes on the last level.
G is minimally connected (if we suppress an edge, the resulting graph is disconnected)

Introductory Notions

  1. Trees
  2. Binary trees
  3. Heaps

Min-Heap generator

Heap

  1. Creation
  2. Insert node
  3. Combination
  4. Extract node

Priority queue

Applications

Dictionary

Properties of Binary Trees

 - Property 1 :: The maximum number of nodes on the level i of a binary tree is 2^i.
- Property 2 :: The maximum number of nodes in a binary tree of height h is 2^(h+1)-1
- Property 3 :: In any nonempty binary tree with n terminal nodes there are n-1 nodes with degree 2.
- Property 4 :: A tree with n vertices has height at least equal to [log n].
- Property 5 :: We define the length of internal paths (I) as the sum of the lengths of the paths from the root to non-terminal (internal) nodes and the length of the external paths (E) as the sum of the lengths of the paths from the root to terminal nodes (leaf or external). In a binary tree with n internal nodes, E=I+2*n.